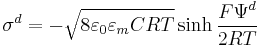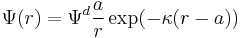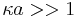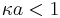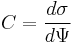Double layer (interfacial)

A double layer (DL, also called an electrical double layer, EDL) is a structure that appears on the surface of an object when it is placed into a liquid. The object might be a solid particle, a gas bubble, a liquid droplet, or a porous body. The DL refers to two parallel layers of charge surrounding the object. The first layer, the surface charge (either positive or negative), comprises ions adsorbed directly onto the object due to a host of chemical interactions. The second layer is composed of ions attracted to the surface charge via the coulomb force, electrically screening the first layer. This second layer is loosely associated with the object, because it is made of free ions which move in the fluid under the influence of electric attraction and thermal motion rather than being firmly anchored. It is thus called the diffuse layer.

Interfacial DL is usually most apparent in systems with a large ratio of surface area to volume, such as colloid or porous bodies with particles or pores (respectively) on the scale of micrometres to nanometres. However, the importance of DLs extends to other systems, e.g., DL is fundamental to the electrochemical behavior of electrodes.

The DL plays a fundamental role in many everyday substances. For instance, milk exists only because fat droplets are covered with a DL that prevent their coagulation into butter. DLs exist in practically all heterogeneous fluid-based systems, such as blood, paints, inks, ceramic slurries and cement slurries.

The DL is closely related to electrokinetic phenomena and electroacoustic phenomena.

The earliest model of the electrical DL is usually attributed to Helmholtz.[1] Helmholtz treated the DL mathematically as a simple capacitor, based on a physical model in which a single layer of ions is adsorbed at the surface.

Later Louis Georges Gouy [2] and David Chapman [3] made significant improvements by introducing a diffuse model of the electrical DL, in which the electric potential decreases exponentially away from the surface to the fluid bulk.

The Gouy-Chapman model fails for highly charged DLs. In order to resolve this problem Stern suggested the combination of the Helmholtz and Gouy-Chapman models, giving an internal Stern layer[4] (i.e. Helmholtz layer), and an outer diffuse layer (i.e. Gouy-Chapman layer).

The combined Gouy-Chapman-Stern model is most commonly used. It still has some limitations, such as

There are more recent theoretical developments that seek to overcome the limitations of the Gouy-Chapman-Stern model. They are reviewed in J. Lyklema's Fundamentals of Interface and Colloid Science.[5]

Contents

Mathematical description

There are detailed descriptions of the interfacial DL in many books on colloid and interface science[6][7][8] and microscale fluid transport.[9][10] There is also a recent IUPAC technical report [11] on the subject of interfacial double layer and related electrokinetic phenomena.

As stated by Lyklema, "...the reason for the formation of a “relaxed” (“equilibrium”) double layer is the non-electric affinity of charge-determining ions for a surface..."[5] This process leads to the build up of an electric surface charge, expressed usually in C/m2. This surface charge creates an electrostatic field that then affects the ions in the bulk of the liquid. This electrostatic field, in combination with the thermal motion of the ions, creates a counter charge, and thus screens the electric surface charge. The net electric charge in this screening diffuse layer is equal in magnitude to the net surface charge, but has the opposite polarity. As a result the complete structure is electrically neutral.

The diffuse layer, or at least part of it, can move under the influence of tangential stress. There is a conventionally introduced slipping plane that separates mobile fluid from fluid that remains attached to the surface. Electric potential at this plane is called electrokinetic potential or zeta potential. It is also denoted as ζ-potential.

The electric potential on the external boundary of the Stern layer versus the bulk electrolyte is referred to as Stern potential. Electric potential difference between the fluid bulk and the surface is called the electric surface potential.

Usually zeta potential is used for estimating the degree of DL charge. A characteristic value of this electric potential in the DL is 25 mV with a maximum value around 100 mV (up to several volts on electrodes[10][12]). The chemical composition of the sample at which the ζ-potential is 0 is called the point of zero charge or the iso-electric point. It is usually determined by the solution pH value, since protons and hydroxyl ions are the charge-determining ions for most surfaces.[5][10]

Zeta potential can be measured using electrophoresis, electroacoustic phenomena, streaming potential, and electroosmotic flow.

The characteristic thickness of the DL is the Debye length, κ−1. It is reciprocally proportional to the square root of the ion concentration C. In aqueous solutions it is typically on the scale of a few nanometers and the thickness decreases with increasing concentration of the electrolyte.

The electric field strength inside the DL can be anywhere from zero to over 109 V/m. These steep electric potential gradients are the reason for the importance of the DLs.

The theory for a flat surface and a symmetrical electrolyte[5] is usually referred to as the Gouy-Chapman theory. It yields a simple relationship between electric charge in the diffuse layer σd and the Stern potential Ψd:

\sigma^d = -\sqrt{{8\varepsilon_0}{\varepsilon_m}CRT}\sinh \frac{F\Psi^d}{2RT}

There is no general analytical solution for mixed electrolytes, curved surfaces or even spherical particles. There is an asymptotic solution for spherical particles with low charged DLs. In the case when electric potential over DL is less than 25 mV, the so-called Debye-Huckel approximation holds. It yields the following expression for electric potential Ψ in the spherical DL as a function of the distance r from the particle center:

{\Psi}(r) = {\Psi^d}\frac{a}{r}\exp({-\kappa}(r-a))

There are several asymptotic models which play important roles in theoretical developments associated with the interfacial DL.

The first one is "thin DL". This model assumes that DL is much thinner than the colloidal particle or capillary radius. This restricts the value of the Debye length and particle radius as following:

{\kappa}a >>1

This model offers tremendous simplifications for many subsequent applications. Theory of electrophoresis is just one example.[13] The theory of electroacoustic phenomena is another example.[14]

The thin DL model is valid for most aqueous systems because the Debye length is only a few nanometers in such cases. It breaks down only for nano-colloids in solution with ionic strengths close to water.

The opposing "thick DL" model assumes that the Debye length is larger than particle radius:

{\kappa}a <1

This model can be useful for some nano-colloids and non-polar fluids, where the Debye length is much larger.

The last model introduces "overlapped DLs".[14] This is important in concentrated dispersions and emulsions when distances between particles become comparable with the Debye length.

Electrical double layers

The electrical double layer (EDL) is a structure which describes the variation of electric potential near a surface, and has a significant influence on the behaviour of colloids and other surfaces in contact with solutions or solid-state fast ion conductors.

The primary difference between a DL on an electrode and one on an interface is the mechanisms of surface charge formation. With an electrode, it is possible to regulate the surface charge by applying an external electric potential. This application, however, is impossible in colloidal and porous DLs, because for colloidal particles, one does not have access to the interior of the particle to apply a potential difference.

EDLs are analogous to the double layer in plasma.

Differential capacitance

Main article: Differential capacitance

EDLs have an additional parameter defining their characterization: differential capacitance. Differential capacitance, denoted as C, is described by the equation below:

C = \frac{d \sigma}{ d \Psi}

where σ is the surface charge and ψ is the electric surface potential.

See also

References

  1. ^ Helmholtz, H. Pogg.Ann. LXXXIX, 211 (1853)
  2. ^ Gouy, G. Comt.Rend. 149, 654 (1909), J.Phys. 4, 9, 457 (1910)
  3. ^ Chapman, D.L. Phil.Mag., 6, 25, 475 (1913)
  4. ^ Stern, O. Z.Electrochem, 30, 508 (1924)
  5. ^ a b c d Lyklema, J. “Fundamentals of Interface and Colloid Science”, vol.2, page.3.208, 1995
  6. ^ Dukhin, S.S. & Derjaguin, B.V. "Electrokinetic Phenomena", J.Willey and Sons, 1974
  7. ^ Russel, W.B., Saville, D.A. and Schowalter, W.R. “Colloidal Dispersions”, Cambridge University Press,1989
  8. ^ Kruyt, H.R. “Colloid Science”, Elsevier: Volume 1, Irreversible systems, (1952)
  9. ^ Bruus, H. (2007). Theoretical Microfluidics. 
  10. ^ a b c Kirby, B.J. (2010). Micro- and Nanoscale Fluid Mechanics: Transport in Microfluidic Devices.. Cambridge University Press. ISBN 978-0521119030. http://www.kirbyresearch.com/textbook. 
  11. ^ ”Measurement and Interpretation of Electrokinetic Phenomena”, International Union of Pure and Applied Chemistry, Technical Report, published in Pure Appl.Chem., vol 77, 10, pp.1753-1805, 2005 (pdf)
  12. ^ V.S. Bogotsky, Fundamentals of Electrochemistry, Wiley-Interscience, 2006.
  13. ^ Hunter, R.J. "Foundations of Colloid Science", Oxford University Press, 1989
  14. ^ a b Dukhin, A.S.; Goetz, P.J. (2002). "Electroacoustic Theory". Ultrasound for Characterizing Colloids. Elsevier. pp. 33. http://www.dispersion.com/pages/theory/psd/modeltheory.html. Retrieved 2007-10-03. 

External links